氢原子镜像波函数方程(化为原子单位制)为:
$$\left( -\frac{d^2}{2dr^2}+\frac{l(l+1)}{2r^2}-\frac{1}{r} \right) P(r)=EP(r)$$
其边界条件为:P(0)=0,P(∞)=0,l为轨道量子数,l=0,1,2,3…分别对应s轨道,p轨道,d轨道,f轨道。。。
本意使用Nomerov方法,数值求解径向波函数,但是对于r=0处有奇点,此处采用差分法求解这个二阶线性非齐次微分方程的本征值问题。Nomerov有五阶精度,而差分只有二阶精度,出现的问题稍后再说。
由于有无穷这个奇点,此处去取无穷等于40作为截短点(l=0时,r=40个玻尔半径时波函数已趋近于零)。利用打靶法确定本征能量E。
程序:(此处取l=1,求p轨道基态波函数,程序未做归一化处理)
Module Number
INTEGER,PARAMETER :: N=10000
INTEGER,PARAMETER :: K=5000
INTEGER,PARAMETER :: L=1
REAL(8),PARAMETER :: h=400.0d0/N
INTEGER :: i,j
END
PROGRAM main
use Number
REAL(8) :: JF,Sum,Y(0:N),E1,E2,Yk,Yk1,EPS
OPEN(10,FILE='Data.txt')
Y(0)=0.d0
Y(1)=0.005d0
EPS=5.d0
Yk=0.d0
E1=-1.d0
E2=0.d0
j=2
CALL CF(Y,E1)
Yk1=Y(k)
E=-1.d0/(2*J*j)
DO WHILE (ABS(E1-E2)>1.d-6)
E=(E1+E2)/2.d0
PRINT*,E
CALL CF(Y,E)
IF (ABS(Y(k)-Yk)
E=-0.1250
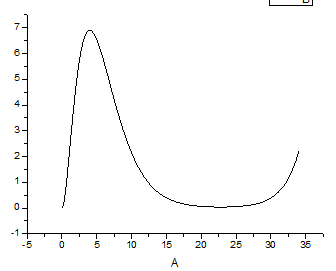
明显,在25个玻尔半径之后,波函数开始上翘,主要原因在于截短点的选取有问题。至于为什么没能达到40个玻尔半径,主要原因则是差分法精度不够。而能量则基本接近解析值。
I value the data on your site. Thnx!
公式很好看。
公式是Late生成的,你的Ctex怎么样了?
“公式很好看。”这一条不是我发的,很奇怪
cdn搞得鬼,中午回去关了去。。。
图是用什么画的?Fortran吗?
fortran得到数据,origin画图,matlab或者mathematica也行
南瓜说的啥……………… 😯