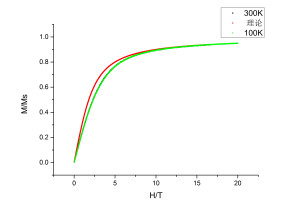
郎之万顺磁理论模拟,利用马尔科夫链,并加以模拟退火的方法,绘制出了顺磁体在外加磁场的作用下,感应磁场的大小。理论上该模型有严格解,从模拟的结果来看,还是比较符合理论的。
基本算法:(1)随机给定系统初态;(2)再次给定每个粒子态;(3)计算每个粒子该次与上次态的能量差dE;(4)dE<0,跃迁至该态,dE>0,按照麦克斯韦分布跃迁;(5)重复2~4步足够多的次数,系统总E达到一个稳定值,获得此时磁畴方向。
module Conts
implicit none
integer,parameter ::Num=1000
integer,parameter ::Step=1000
real(8),parameter ::pi=3.1415926d0
real(8),parameter ::miu=1.d0 !9.27d-24
real(8),parameter ::kb=1.d0 !1.38d-23
end
program Main
use Conts
real(8) ::T=100.d0
real(8) :: H,dH,addField,Eh,rou
integer ::i,j
open(10,file="data.dat")
call RANDOM_SEED()
dH=0.02d0*T
do i=1,step
H=real(i)*dH
Eh=addField(H,T)/(H*miu)
rou=miu*H/(kb*T)
write(10,*)H/T,-Eh,cosh(rou)/sinh(rou)-1.d0/rou
enddo
end
real(8) function addField(H,T)
use Conts
integer ::Moves=1000
integer ::i,j
real(8) ::E(Num),r1,r2,r3,temp,dE,p
real(8) ::H,T
do i=1,Num
call RANDOM_NUMBER(r1)
call RANDOM_NUMBER(r2)
E(i)=-H*miu*cos(r1*pi)*sin(r2*pi)
enddo
addField=0.d0
do i=1,Moves
do j=1,Num
call Random_number(r1)
call Random_number(r2)
Temp=-H*miu*cos(r1*pi)*sin(r2*pi)
dE=Temp-E(j)
if (dE<0) then
E(j)=Temp
else
p=EXP(-dE/(T*kb))
call Random_number(r3)
if (r3<=p) E(j)=Temp
endif
enddo
if (i>Moves/2) addField=addField+sum(E)
enddo
addField=addField/(Num*Moves/2.)
end